阿尔伯特·爱因斯坦在1915年提出了广义相对论，该理论主要基于质量和能量使四维时空结构扭曲这一事实，从而彻底改变了引力的概念。

其潜在的几何或数学公式要归功于一位名叫乔治·弗里德里希·伯恩哈德·黎曼的数学家，他构造了一类几何（或椭圆几何），与欧几里得几何（或平面几何）不同，它用以处理高维和超曲面。

黎曼是德国数学家，在哥廷根大学学习和任职。在哥廷根，他遇到了一位伟大的老师，卡尔·弗里德里希·高斯。他还在柏林大学度过了一段时间，在那里他遇见了其他杰出的导师，包括雅可比、狄利克雷和爱森斯坦。他从爱森斯坦那里学习椭圆函数理论，而对他影响最大的是狄利克雷。

根据费力克斯·克莱茵的说法：

高斯开始思考欧几里得几何的有效性比黎曼早很多年。高斯与黎曼分享了他的好奇心，请他重新制定欧几里得几何的基础，以一种可以将曲面纳入通常三维之外的方式。

在那个时代，对第四维度的思考被认为是荒谬。约翰·沃利斯在他的《代数论》中把第四维度描述为“自然界中的怪物”。与此同时，波尔约和洛巴切夫斯基尝试用双曲几何的形式推广他们的非欧几何，这为黎曼提供了灵感。

黎曼突破性的演讲

为了赢得哥廷根大学的永久职位，黎曼必须写一篇长篇论文，还要做一次演讲。他花了两年半的时间完成了关于函数的三角级数可表示性的论文。

1854年，他发表了题为“关于几何基础的假设”的演讲，这次演讲是如此非凡，以至于成为一种新的几何，即黎曼几何的基石。

在讲座开始时，他重点定义n维空间、测地线、曲率张量等。在最后一部分，他试图将他的几何与现实世界联系起来。听众中的许多科学家听不懂这个讲座，因为它太超前了，不是每个人都能理解和欣赏的。然而，只有高斯完全理解黎曼的几何本质。

M. Monastyrsky在《黎曼，拓扑和物理》中的一段提到，

加来道雄在他的《超空间》一书中写道，

欧几里得几何与黎曼几何之比较

欧几里得几何适用于平面空间，如点、线、平面等；黎曼几何适用于曲面空间，如圆柱、球面、环面等。

• 欧几里得的第五个公设——平行公设在椭圆几何中是完全被否定的。因为它说的是“通过一点，而不是在给定的直线上，只有一条直线与给定的直线平行”。而在曲线几何中，没有平行线。

• 在平面空间中，三角形三个角的和总是等于180°，而在弯曲空间中，三角形的和不是大于就是小于180°，因为三角形的边在球面上是向外弯曲的，在双曲线上是向内弯曲的。

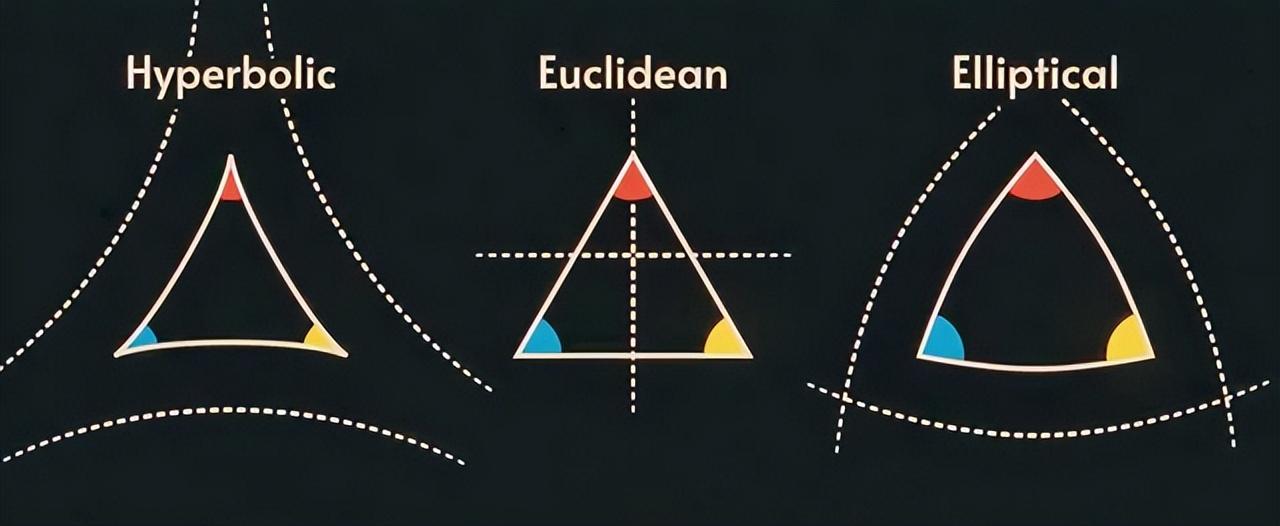
• 在平坦空间中，两点之间的最短距离是一条直线，可以用距离公式计算，而在弯曲空间中，直线被称为测地线，它表示局部距离最小化路径。有时，两点之间存在多个测地线。

高斯在他的曲面理论中描述了一个矢量在一维中有两个分量，即大小和方向。黎曼将这一概念扩展到更高的维度，并证明了一个向量将拥有六个独立的分量来描述三维空间中任何点的曲率。同样，在四维空间中，有20个独立的分量。

黎曼几何如何帮助爱因斯坦推广他的引力理论？

当爱因斯坦提出狭义相对论时，他主要关注的是它的物理性质和解释，而不是任何数学构造。他以前的老师赫尔曼·闵可夫斯基提出了狭义相对论的几何学，并将空间和时间描述为一个单一的实体。

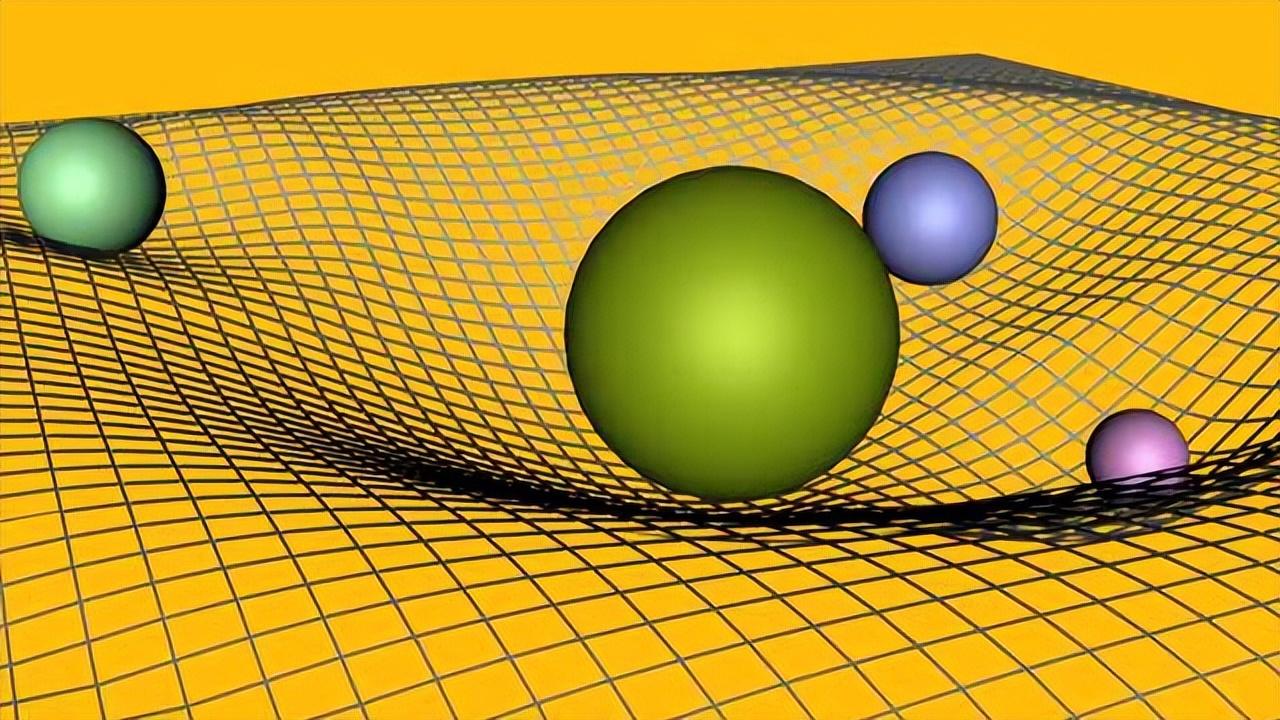
因此，对于他的一般理论，爱因斯坦没有意识到控制大质量物体周围引力场影响的数学规律。

他逐渐意识到，必须抛弃用单一标量场来描述引力，而需要一种新的几何语言。为此，他向在苏黎世理工学院工作的数学家朋友马塞尔·格罗斯曼寻求帮助。他说：“格罗斯曼，你得帮帮我，否则我会发疯的。”格罗斯曼指示他去寻找黎曼提出的新型几何。

黎曼新的数学框架对爱因斯坦来说是一个意外的幸运，因为它引导他得出这样的结论：引力实际上是时空曲率的结果。时空曲率越大，它受到的引力就越大。

正如米斯纳、索恩和惠勒所总结的，

当爱因斯坦意识到黎曼几何是广义相对论的精确数学工具时，接下来的三年是他研究生涯中最艰苦的时期。“我累坏了。但成功是光荣的，”爱因斯坦在1915年说。

爱因斯坦对黎曼的贡献赞不绝口，

汉斯·弗罗伊登塔尔在传记中写道：

黎曼在数论、分析、函数、曲面的拓扑性质等方面做出了有价值的贡献。

1862年，他患上了严重的感冒，最终患上了肺结核。最后，他于1866年在意大利马焦雷湖的塞拉斯卡去世，年仅39岁。